Whilst you have a look at your surrounding atmosphere, it would look like you’re residing on a flat aircraft. Finally, for this reason you’ll be able to navigate a brand new town the usage of a map: a flat piece of paper that represents all of the puts round you. That is most likely why some other people up to now believed the earth to be flat. However most of the people now know this is some distance from the reality.
You continue to exist the skin of a large sphere, like a seashore ball the scale of the Earth with a couple of bumps added. The skin of the sector and the aircraft are two conceivable 2D areas, which means you’ll be able to stroll in two instructions: north and south or east and west.
What different conceivable areas may you be residing on? This is, what different areas round you’re 2D? For instance, the skin of a large doughnut is any other 2D house.
Via a box referred to as geometric topology, mathematicians like me find out about all conceivable areas in all dimensions. Whether or not seeking to design safe sensor networks, mine information or use origami to deploy satellites, the underlying language and concepts usually are that of topology.
The form of the universe
Whilst you glance across the universe you are living in, it looks as if a 3-d house, similar to the skin of the Earth looks as if a 2D house. Then again, similar to the Earth, in case you had been to have a look at the universe as a complete, it generally is a extra sophisticated house, like a large 3-d model of the 2D seashore ball floor or one thing much more unique than that.
A doughnut, also referred to as a torus, is a form that you’ll be able to transfer throughout in two instructions, similar to the skin of the Earth.
YassineMrabet by means of Wikimedia Commons, CC BY-NC-SA
When you don’t want topology to resolve that you’re residing on one thing like a large seashore ball, understanding all of the conceivable 2D areas can also be helpful. Over a century in the past, mathematicians found out all of the conceivable 2D areas and plenty of in their houses.
Previously a number of many years, mathematicians have realized so much about all the conceivable 3-d areas. Whilst we should not have a whole figuring out like we do for 2D areas, we do know so much. With this information, physicists and astronomers can attempt to resolve what 3-d house other people in fact are living in.
Whilst the solution isn’t totally recognized, there are lots of intriguing and sudden chances. The choices develop into much more sophisticated in case you believe time as a size.
To look how this may paintings, notice that to explain the positioning of one thing in house – say a comet – you wish to have 4 numbers: 3 to explain its place and one to explain the time it’s in that place. Those 4 numbers are what make up a 4D house.
Now, you’ll be able to believe what 4D areas are conceivable and through which of the ones areas do you are living.
Topology in upper dimensions
At this level, it’s going to look like there’s no explanation why to believe areas that experience dimensions higher than 4, since that’s the perfect possible size that may describe our universe. However a department of physics referred to as string idea means that the universe has many extra dimensions than 4.
There also are sensible programs of interested by upper dimensional areas, reminiscent of robotic movement making plans. Assume you are attempting to know the movement of 3 robots shifting round a manufacturing facility ground in a warehouse. You’ll put a grid at the ground and describe the placement of each and every robotic through their x and y coordinates at the grid. Since each and every of the 3 robots calls for two coordinates, you’ll want six numbers to explain all the conceivable positions of the robots. You’ll interpret the conceivable positions of the robots as a 6D house.
Because the selection of robots will increase, the size of the distance will increase. Factoring in different helpful knowledge, such because the places of hindrances, makes the distance much more sophisticated. With the intention to find out about this downside, you wish to have to review high-dimensional areas.
There are numerous different medical issues the place high-dimensional areas seem, from modeling the movement of planets and spacecraft to seeking to perceive the “shape” of enormous datasets.
Tied up in knots
Any other form of downside topologists find out about is how one house can take a seat inside of any other.
For instance, in case you cling a knotted loop of string, then we have now a 1D house (the loop of string) inside of a 3-d house (your room). Such loops are referred to as mathematical knots.
The find out about of knots first grew out of physics however has develop into a central house of topology. They’re crucial to how scientists perceive 3-d and 4D areas and feature a lovely and delicate construction that researchers are nonetheless seeking to perceive.
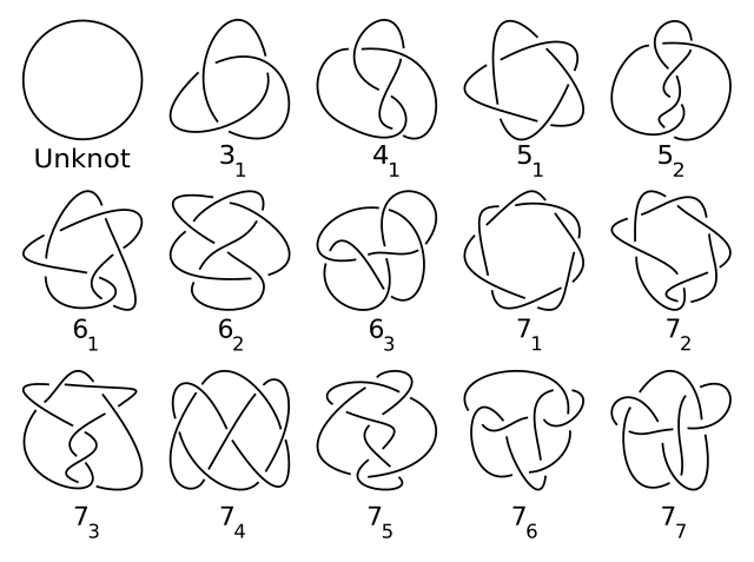
Knots are examples of areas that take a seat inside of different areas.
Jkasd/Wikimedia Commons
As well as, knots have many programs, starting from string idea in physics to DNA recombination in biology to chirality in chemistry.
What form do you continue to exist?
Geometric topology is a gorgeous and complicated topic, and there are nonetheless numerous thrilling questions to respond to about areas.
For instance, the graceful 4D Poincaré conjecture asks what the “simplest” closed 4D house is, and the slice-ribbon conjecture targets to know the way knots in 3-d areas relate to surfaces in 4D areas.
Topology is lately helpful in science and engineering. Unraveling extra mysteries of areas in all dimensions will probably be valuable to figuring out the arena through which we are living and fixing real-world issues.




