Listed below are the solutions to the festive maths quiz I set on December 23. I’m hoping you loved it.
nestdesigns/Shutterstock
Puzzle 1: You might be given 9 gold cash that glance an identical. You might be informed that one in all them is pretend, and that this coin weighs lower than the actual ones. The use of a collection of out of date steadiness scales, what’s the smallest collection of weighings you want to resolve which is the pretend coin?
Answer: You’ll do that in simply two weighings:
(1) Divide the 9 cash into 3 units of 3, and make a selection two of those units to weigh towards one some other. If one set is lighter than the opposite, then the pretend is this sort of 3 cash. If the 2 units weigh the similar, then the pretend is within the 3 unweighed cash.
(2) Now take the set with the pretend coin, and weigh two of its cash towards each and every different. If one is lighter, that’s the pretend. In the event that they weigh the similar, then the pretend is the 3rd coin.
Puzzle 2: You’ve been transported again in time to lend a hand cook dinner Christmas dinner. Your process is to bake the Christmas pie, however all you’ve were given is 2 egg-timers: person who occasions precisely 4 mins, and person who occasions precisely seven mins. How are you able to time ten mins precisely?
Answer: There are a couple of solutions to this puzzle, however supposing the chef desires you cook dinner this pie as briefly as conceivable, right here’s the best way to do it:
– Get started each timers on the identical time.
– As soon as the four-minute timer has completed, the seven-minute timer can have 3 mins to head. At this level, put the pie within the oven.
– As soon as the remainder 3 mins at the seven-minute timer has completed, flip the seven-minute timer over.
– Let the seven-minute timer run its complete route, then take the pie out right away. The pie can have been within the oven for ten mins precisely.

Dasha Efremova/Shutterstock
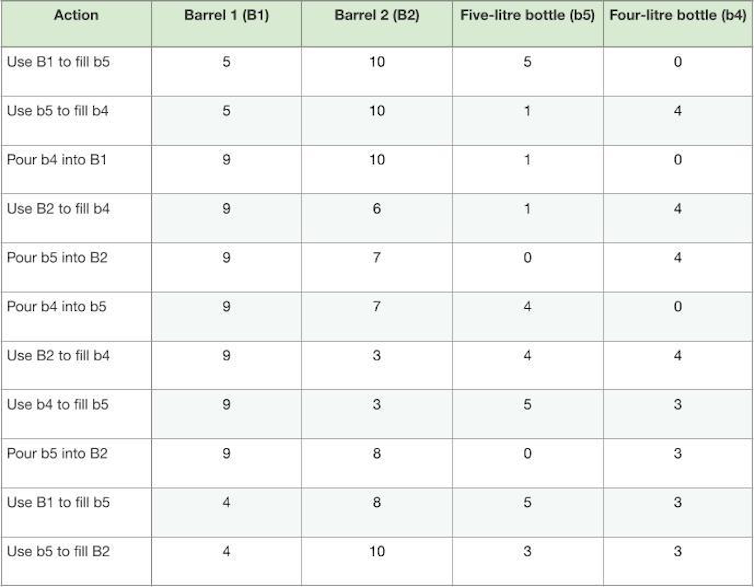
Puzzle 3: You are actually entrusted with allocating the mulled wine, which is these days in two complete ten-litre barrels. The chef arms you one five-litre bottle and one four-litre bottle, each empty. He orders you to fill the bottles with precisely 3 litres of wine each and every, with out losing a drop. How are you able to do that?
Answer: Here’s a answer in 11 steps (see desk beneath), recording the amounts of mulled wine in each and every barrel and bottle. B1 and B2 are the 2 ten-litre barrels; b5 and b4 are the five-litre and four-litre bottles respectively.
Be aware: You may have discovered a faster answer than mine, however that is what I may get a hold of!
Puzzle 4: Think there are 100 days of Christmas. At the n-th day, you obtain £n as a present, starting from £1 at the first day to £100 at the ultimate day. Are you able to calculate the full amount of cash you’re given, with out laboriously including all 100 numbers in combination?
Answer: When Carl Friedrich Gauss was once posed this query by way of his maths instructor, the budding mathematician is claimed to have carried out the next calculation:
Let s be the sum of the primary 100 digits. Then we will be able to write: s = 1 + 2 + 3 + 4 + … + 99 + 100
However we will be able to additionally write this backwards: s = 100 + 99 + 98 + … + 4 + 3 + 2 + 1
If we now upload those two equations vertically time period by way of time period, we see that the left hand aspect is s + s = 2s.
At the right-hand aspect, including vertically once more, the sum of each and every two phrases is all the time the similar, specifically 101 (1 + 100, 2 + 99 and so forth). And there are 100 phrases in all – so the simple calculation for the full at the right-hand aspect is 100 * 101 = 10,100.
Due to this fact: 2s = 10,100, and s = 5,050. The overall amount of cash you’re given is £5,050.
Puzzle 5: Right here’s a Christmassy collection of numbers. The primary six within the collection are: 9, 11, 10, 12, 9, 5 … (Be aware: the 5th quantity is 11 in some variations of this puzzle.) What’s the subsequent quantity on this collection?
Answer: This collection is the collection of letters in each and every consecutive provide given over the 12 days of Christmas. So the solution is 5, for swans. Right here’s the total record:
Partridge (9), turtle doves (11), French hens (10), calling birds (12), gold rings (9, or 11 for individuals who sing “golden”), ducks (5), swans (5), maids (5), girls (6), lords (5), pipers (6), drummers (8).
Be aware: this would possibly appear to be a non-mathematical puzzle, however maths – and extra extensively, vital and inventive pondering – partly will depend on recognizing patterns that would possibly glance a bit of tenuous in the beginning. Recruitment to the Allies’ code-breaking headquarters Bletchley Park throughout the second one global warfare was once in part in accordance with the facility to resolve a cryptic crossword.

Garashchuk/Shutterstock
Puzzle 6: Which of the next 100 statements is the one true one?
Precisely one commentary on this record is fake.
Precisely two statements on this record are false.
… and so forth till:
Precisely 99 statements on this record are false.
Precisely 100 statements on this record are false.
Answer: Handiest the 99th commentary on this record is correct. Since there are 100 statements, and the n-th commentary asserts that precisely n statements within the record are false, this may simplest be true when n = 99.
Puzzle 7: You and your pals Arthur and Bob are dressed in Christmas hats which are both purple or inexperienced. No one can see their very own hat however you’ll all see the opposite two. Arthur’s and Bob’s hats are each purple.
You might be all informed that a minimum of some of the hats is purple. Arthur says: “I do not know what colour my hat is.” Then Bob says: “I do not know what colour my hat is.” Assuming your pals have impeccable common sense, are you able to deduce what color your Christmas hat is?
Answer: Your hat will have to be purple. In case your hat had been inexperienced, then each Arthur and Bob would see one inexperienced and one purple hat. So when Arthur says that he doesn’t know the color of his hat, Bob may right away deduce that his hat was once purple. However since Bob doesn’t know the color of his hat, Bob will have to be seeing two purple hats, and so you’ll deduce that your hat is purple.
Puzzle 8: There are 3 bins beneath your Christmas tree. One incorporates two small gifts, one incorporates two items of coal, and one incorporates a small provide and a work of coal. Each and every field has a label on it that displays what’s inside of – however the labels have were given blended up, so each and every field these days has the fallacious label on it.
You might be informed that you’ll succeed in in and take out one object from only one field. Which field must you select to be able to then be capable to transfer the labels in order that each and every label accurately corresponds to the contents of its field?
Answer: Since the entire bins have the fallacious labels, that should you open the field these days labelled as containing one small provide and one piece of coal, you are going to both see two small gifts or two items of coal.
Think you open it and notice two small gifts. Then the label of 2 small gifts will have to be fastened to this field. And because you additionally know that each and every field firstly had the fallacious label, the label of 1 small provide and one piece of coal must pass at the field these days labelled two items of coal. In spite of everything, the 2 items of coal label belongs to the field firstly labelled two small gifts.
Puzzle 9: There’s a one-litre bottle of orange juice and a one-litre bottle of apple juice within the kitchen. Jack places a tablespoon of orange juice into the bottle of apple juice, then stirs it round so it’s flippantly blended. Now Jill takes a tablespoon of liquid from that apple juice bottle places it again within the bottle of orange juice. Is there now extra orange juice within the bottle of apple juice, or extra apple juice within the bottle of orange juice?
Answer: They’re the similar. This can be a great instance of “invariance” – a time period that comes up so much in arithmetic.
In spite of everything the including of tablespoons of juice and the entire blending, the quantity of orange juice within the apple juice bottle will have to have changed the same quantity of apple juice that was once firstly within the apple juice bottle, since the quantity of liquid in each and every bottle continues to be one litre (they’ve remained invariant).
This clarification can really feel unsatisfactory whilst you first learn it. However exploiting the ability of invariance lets you deduce that the quantities will have to be the similar, with none calculation.

joto/Shutterstock
Puzzle 10: In Santa’s house the town, all banknotes raise footage of both Santa or Mrs Claus on one aspect, and photographs of both a gift or reindeer at the different. A tender elf puts 4 notes on a desk appearing the next footage on this order:
Santa | Mrs Claus | Provide | Reindeer
Now an older, wiser elf tells him: “If Santa is on one side of the note, a present must be on the other.” Which notes will have to the younger elf flip over to verify what the older elf says is correct?
Answer: First, the younger elf must flip over the banknote with Santa on it. If there isn’t a gift at the different aspect, then the older elf is mendacity. Subsequent, the younger elf must flip over the reindeer banknote to verify that Santa isn’t at the different aspect. Once more, if Santa had been at the different aspect, the older elf could be mendacity.
It could be tempting to show over the prevailing banknote. However the older elf simplest says “if Santa, then present”, which doesn’t indicate “if present, then Santa”. So it doesn’t topic whether or not Santa or Mrs Claus is at the different aspect of the current banknote – and it additionally doesn’t topic what’s at the different aspect of the Mrs Claus banknote, since the older elf doesn’t say anything else about the ones notes.
Bonus puzzle answer
Santa travels on his sleigh from Greenland to the North Pole at a pace of 30 miles in keeping with hour, then right away returns from the North Pole to Greenland at a pace of 40 miles in keeping with hour. What’s the moderate pace of Santa’s complete travel?_
Answer: This puzzle is most likely an instance of what psychologist Daniel Kahneman referred to as Pondering Rapid and Gradual. Our fast-thinking device would possibly say “just take the average”, and so we’d wager 35 miles in keeping with hour. An inexpensive solution, however fallacious.
Our slower-thinking device – which is effortful to make use of, requiring gear like algebra and important pondering – is wanted right here. First, let’s arrange some variables:
– let d be the gap from Greenland to the North Pole.
– let t₁ be the time taken at the out-journey.
– let t₂ be the time taken at the go back travel.
The use of the usual equation “speed = distance divided by time”, we will be able to say:
30 = d/t₁ and 40 = d/t₂
Rearranging those equations, we additionally know that t₁ = d/30 and t₂ = d/40
Since Santa travels the similar distance there and again, his general distance travelled is second. And the common pace for the full travel is that this general distance divided by way of the full time taken: second/(t₁ + t₂)
The use of all the above, we will be able to say the common pace of Santa’s travel is second/(d/30 + d/40)
Now, (d/30 + d/40) = (4d/120 + 3d/120) = 7d/120
So Santa’s moderate pace = second / (7d/120) = 240/7 = 34.3
On this equation, the ‘d’s cancel out. This implies we will be able to determine the common pace of the adventure with out understanding both the gap or the time it took Santa to make his travel. That is the ability of algebra: it lets you use and manipulate amounts, the use of them as position holders even whilst you don’t know what the amounts are.
The solution is that Santa travelled at a median pace of 34.3 miles in keeping with hour.






